Hello friends,
We've just started a new section that is an extension on function study and introduces some new concepts. As you know, a function is an expression that has a distinct output for every input. We've already used four operations (addition, subtraction, multiplication, and division) in function annotation, and composition is the fifth. When composing functions, one function is applied into another and their equations are plugged in to find the answer. In other words, the output of one functions becomes the input for another.
Here's an example:

Keep in mind that the notation of (f+g)(x) is the same as f(x) + g(x). The
composite function is (f+g) and it dictates what operation we will use in our composition.
Now let's begin to plug in for x using our original equations from above.
When we combine like terms, our answer is:
In conclusion, we plugged in the equation of one function into that of the other function and looked at our composite function to determine what operations we would use. This particular problem involved addition, let's try one with a different operation:
Given f (x) = 2x – 1 and g(x) = (1/2)x + 4, find ( f o g)(x)
This problem looks more challenging, but we can do it! Notice that an open circle denotes multiplication in composition.
1. Isolate the composite function and break it down into a form that involves two steps.
( f o g)(x) = f (g(x))
2. Now we can see that we first have to plug in the equation for g(x), the inside function.
= f ((1/2)x + 4)
3. Now we plug in the equation for f(x), the outside function.
= 2((1/2)x + 4) – 1
4. Simplify
= x + 8 – 1
And our answer is x + 7!
Now we'll look at composition from a slightly different angle. Decomposing compositions involves working backwards from a given equation to find the two functions that match it.
For example:
Here is the function we are asked to decompose.
1. While we are working backwards, if we use the first step from our composition problems and determine our composite function, this problem becomes easier to solve.
2. Now that we know our composite function, we can begin to break down our original equation into two functions. Because (x-4) is squared, we know that our outside function, f(x) must also be squared This is because plugging in for f(x) is our last step and no matter what we plug in for "x", the function will ultimately be squared like in our original equation.
3. Now we can look for the other function. We know that what we plug in for "x" must match the original equation, and so that must be:
So those are our two functions! Make sure you check your answers by using the composite function to plug in for each function.
The last lens through which we've viewed compositions so far looks at the relationship between functions. An
inverse function is an expression that involves functions that have reverse qualities. In other words, if (a,b) is on f(x), then (b,a) is on g(x).
In another example, the inverse of f(x) is shown as :
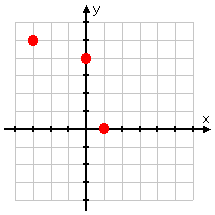
In class, we looked at graphs of inverse functions and looked at the points of one function to determine those of another. Here's an example:
If we're given the points:
{ (1, 0), (–3, 5), (0, 4) }
then the inverse points would be:
{ (0, 1), (5, –3), (4, 0) }
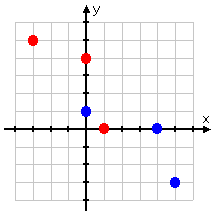
When plotting inverse relations, there is a line of symmetry. Inverse relations are symmetric over the line y=x.
When looking at inverses algebraically, the process is a bit different. When inverses are composed together, the answer is "x".
Here, have a look:
Find ( f o g)(x) and ( g o f)(x) when f (x)=x+3 and g(x)=x-3
1. Plug in g(x) into f(x):
f (x-3)
2. Plug that into "x" in equation for f (x):
f (x-3) +3
3. Simplify:
=x
When we do the same steps and modify them slightly for ( g o f)(x), we get the same answer!
1. g(x+3)
2. g(x+3) -3
3. =x
Now we've reviewed how to compose, decompose, and determine the inverses of functions. I hope this helped!